PRINT VERSION - Graphing Skills

This toolkit will help middle school and high school students gain confidence in creating and reading graphs. Students will create graphs that are personal and relevant to their lives and interpret provided graphs. This toolkit is created by high school math teachers and is designed to prepare a student for high school level graph fluency.

Goals and Standards

---

Colorado Academic Standards:

• 5.G.A.2 The Number System: Represent real world and mathematical problems by graphing points in the first quadrant of the coordinate plane, and interpret coordinate values of points in the context of the situation.
• 6.EE.C. Expressions & Equations: Represent and analyze quantitative relationships between dependent and independent variables.
• 6.NS.C.8 Geometry: Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate.
• HS.F-IF.B. Interpreting Functions: Interpret functions that arise in applications in terms of the context.

Mathematical Practice Standards:

• Math Practice MP2. Reason abstractly and quantitatively.
• Math Practice MP3. Construct viable arguments and critique the reasoning of others
• Math Practice MP4. Model with mathematics.

Learning Goal:

• Students will create and analyze graphs that represent their lives to prepare themselves for high school level graphing skills.

Next Section:

Progression of Skills (outline)

Before the lesson:

• Students should be fluent in simplifying numerical expressions. They should also have a firm grasp on variables as numbers, including exposure to (but not mastery of) equivalent expressions with positive integers. If a student can complete the pre-assessment, they are ready for this toolkit lesson.

During this toolkit lesson:

• Focuses on identifying and generating equivalent expressions, including understanding the rules for multiplying negative numbers, distribution, factoring and combining like terms.

After the lesson:

• Students are ready to learn to solve linear equations in one variable.

Lesson Activity 1

Directions for Intervention Activity:

• Activity 1 Hand out
• Activity 1 Student Answers

1. Warm-up: 
   1. It is highly recommended that the instructor completes the warm-up and Activity 1 in its entirety before helping students.
   2. Additionally, in order to interpret these later, the number lines must include an abbreviation for each of the rankings. 
   3. The instructor should be ready to be flexible in Activity 1 based on how students create their number lines. In particular, if students write their abbreviations above the number line, it will end up in the coordinate grid (if they are the y-axis). If necessary, have students rewrite the abbreviations in a way that doesn’t interfere with the later graphing. 
   4. Two examples are shown below:
       
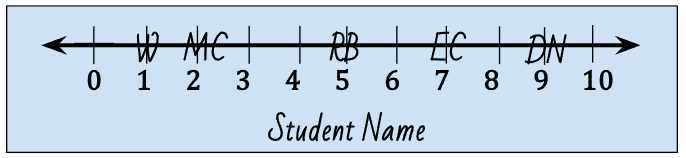
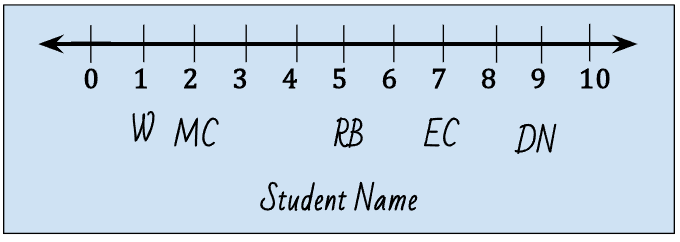
   5. Please refer to the image on the next page which demonstrates a finished product.
2. Activity 1: Friend Graphs
   1. In this activity students will be creating a quadrant 1 graph using two number lines while working in pairs. Additionally, students will interpret and analyze graphs.
   2. Students should be placed into partners. If this toolkit is being used on a one-on-one intervention, the instructor should also complete the warm-up task.
   3. Partners will answer questions 1 and 2 on the Activity 1 handout. In question 1, any observations are valid! Hopefully partner teams are discussing their rankings interpersonally. Perhaps students used different abbreviations. If so, encourage students to come to an agreement over which abbreviation should be preferred. It is important for the abbreviations to be succinct, so they fit on the graph.
   4. Question 2 is hoping to have students rely on their past knowledge of number lines to determine the largest distance between two ideas. 
   5. Next, students will construct their friendship plots. Give students time to read the instructions and ask questions. Allow them to work without guidance at first. As you monitor, check that the number lines are meeting at a right angle. 
   6. Once a group has their number lines joined and taped/glued onto a separate, blank piece of paper, have them read the instructions for plotting. Students should be able to do this process independently as well. Once teams have two points plotted, ask them for an explanation on why they placed that point where it is. (Keep in mind, our data “points” are actually abbreviations!)
   7. If two students have two separate items that have the exact same ranking (3,4) and (3,4) for example, let them brainstorm a strategy to display this on the graph. One idea could be to write the two abbreviations with a slash.
   8. The end goal should look something like this:
      
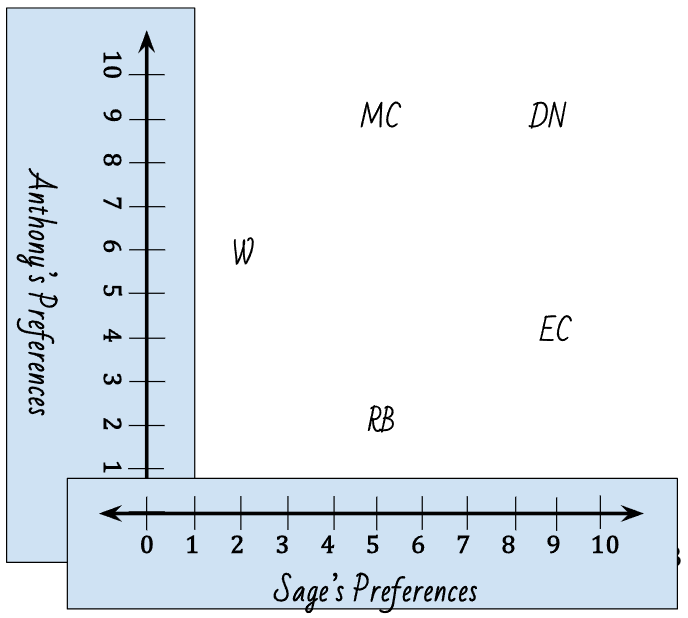
   9. If a partner team is struggling with this new concept, try to focus your questioning around each number line being each person’s ranking. 
   10. After graphing, students are asked to find the x, y coordinate pairs for each of their data points. Students may ask to look at their warmup to confirm data points. If a point is ambiguously placed in a way that is difficult to interpret, have students refer back to the numerical rankings.
   11. Through the pre-assessment, hopefully you have a strong idea of how challenging this task will be. It is appropriate to model this process for one or two points for a partner team that struggles with this skill. However, it is recommended to refer to each coordinate as each person’s ranking to emphasize the concept.
   12. Once complete, you can have teams check each other's points in a group of 4, or you can check the points to confirm.
3. If you are working with a class of students, now would be a good time to allow students to see each other’s work. A gallery walk is one useful strategy for this. 
   1. Additionally, it may be useful to unpack some of the student-created graphs by displaying one and asking the whole class “What did Susie rank winter on a scale of 1-10?” Allow students to think privately first, then ask a student to show their thinking in addition to their answer. A key point to uplifted is that we have to go to “Susie’s Axis” to find her ranking.
   2. Students will practice this type of interpretation in question 6. This will give the instructor the opportunity to narrow in on any misconceptions that may be happening for individuals.
   3. Questions 7, 8 and 9 are conceptual questions to push the abstract thinking of students.
   4. In 7 and 8, encourage students to identify the points they agreed and disagreed on in their own graphs if they are struggling with the questions.
   5. In Question 9, we are hoping to see the misconception that the distance from the x-axis is the x-coordinate. This is not true, but is the most common mistake we anticipate. Lead students back to their number lines. Each rating was the distance from zero on that line.
   6. Furthermore, in part b. Emphasize that students should be giving step-by-step instructions to help the imaginary team. It is encouraged to have students explain the process to the instructor or each other instead of writing every step.

Activity 2

Directions for Intervention Activity:

• Activity 2 Hand out (Answer Key guidance provided in Instructor’s Guide)

1. In this activity students will be creating a quadrant 1 graph which models their experiences in math class over their life. Students will also practice the procedure of identifying coordinate pairs.
2. Activity 2: Story of Your Math Life
   1. In this activity students will first reflect on what their experience has been like in mathematics. Many students have never considered this in depth, but most students will have some positive and some negative memories. Push students to really consider how their math experience has gotten better and worse over time. Check-in with each student to read their answer to question 1, specifically part c.
   2. If teaching in a classroom environment, have everyone pause on question 2 and field brainstormed answers to what the axes could represent. Remind students of the previous activity where each axis is a different number line with a different measurement.
   3. The x-axis will be time as this is conventional in math. Make sure to correct students who put time on the y-axis. Students are welcome to notate this as their age, or as the grade they were in. 
   4. The y-axis can be any of the brainstormed ideas. Joy, fun, confidence and success are possibilities for the categorization of the y-axis. Ideally, different students have different ideas.
   5. Then, as a class, consider how the y-axis should be ranked. It is likely students will suggest that the y-axis is ranked from one to ten, similar to the last activity.
   6. To create the graph, have students mark their answers to question 1.a and 1.b, then have them fill in the graph with a line or curve that represents what happens in between. Remind students that this is just a general idea of what it’s been like, not necessarily a perfectly precise summary.
   7. Next, have students pick out some points that are on their graphs. Students may have few points that can be clearly read. Instruct students to approximate precisely. Utilize the space on the number line to help students visualize this.
   8. Question 7 asks them to pick any point that is not on their line. When working with students emphasize that there are so many points on this graph that we could pick. We have two types of points present. Some that apply to you and your life, and some that do not represent your experience.
   9. Finally, question 8 asks students to reverse this process and think about just a point. If a student is struggling, suggest they graph it first and then interpret it.

• Catalyzing Change in High School Mathematics
  • Pg. 28 - Developing a positive mathematical identity and agency
  • Pg. 57 - Quantitative Literacy
    • Create and interpret visual representations
    • “Focus 2” - Visualizing and summarizing data
• Roles of Representations in School Mathematics
  • Preface (ix) importance of the perspective of students (given in context of how they learn but relevant to the experiences of the student)
  • Chapter 19 (pg. 238) Realistic Mathematics Principles
    • 1. Learning math involves construction
    • 3. Math learning is promoted by reflection
• UDL: 
  • Optimize individual choice and autonomy (checkpoint 7.1)
  • Optimize relevance, value, and authenticity (checkpoint 7.2)
  • Foster collaboration and community (checkpoint 8.3)
  • Develop self-assessment and reflection (checkpoint 9.3)
• Inspiration Homie Scatterplots